Функция поиск решения в excel. включение, пример использования со скриншотами

Подготовка таблицы

Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

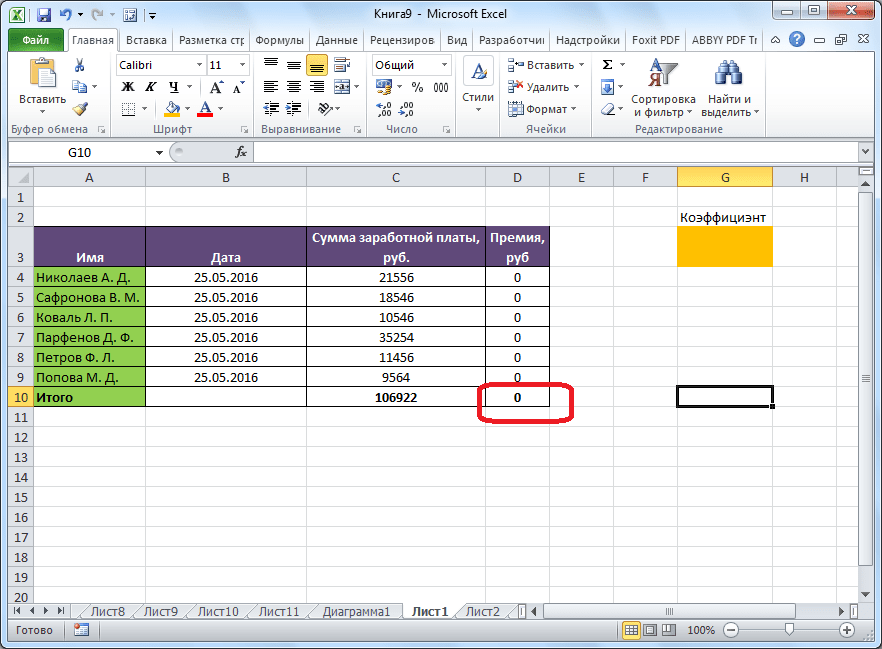
Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

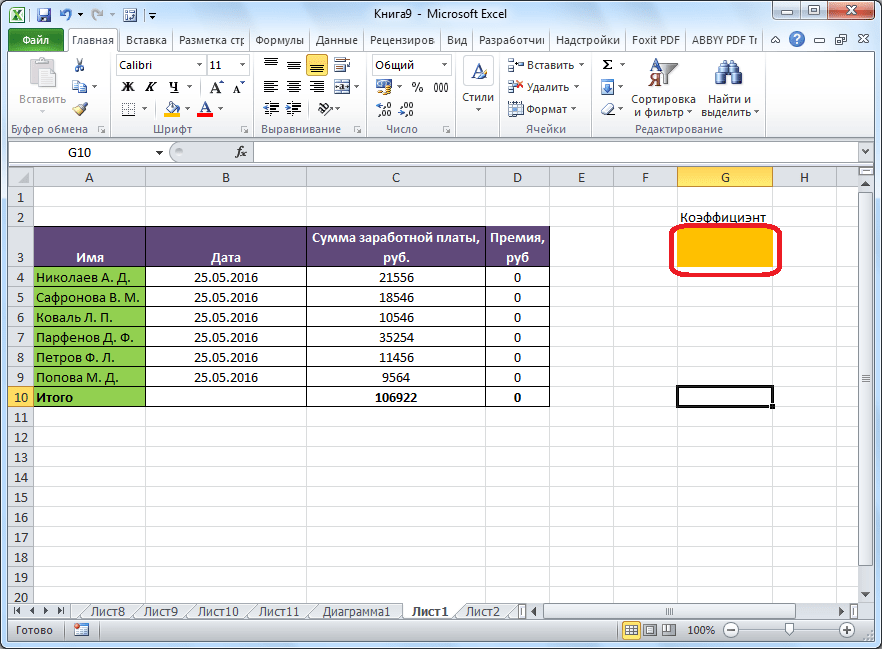
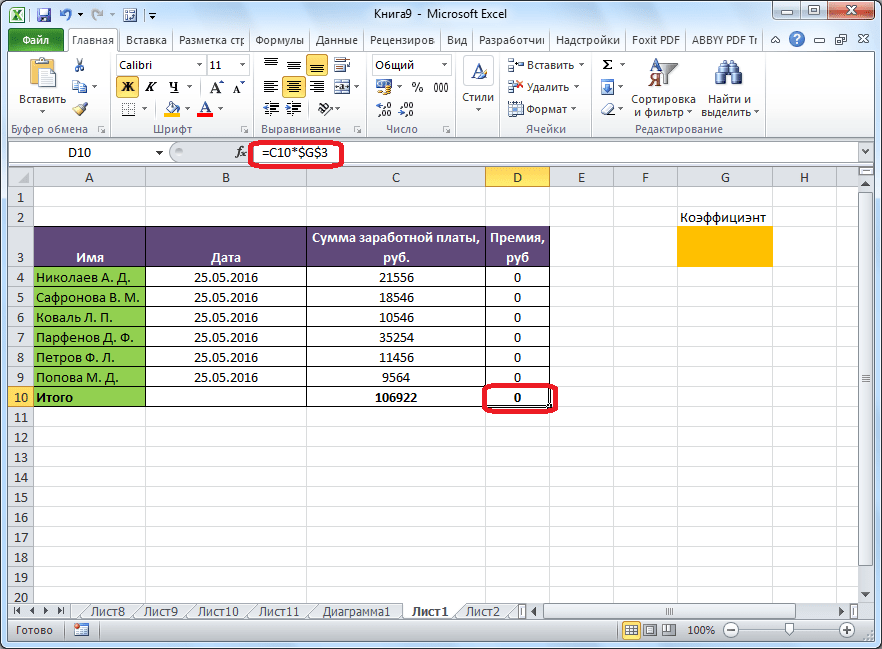
Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.

Подбор параметра и решение уравнений в Excel

Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:

• y =7 является функцией x ;
• нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

1. Заполните ячейки листа, так как показано на рисунке:
2. Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
3. В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

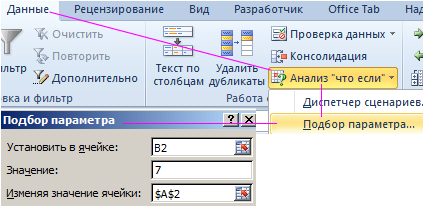
В результате мы получили правильное значение 3.

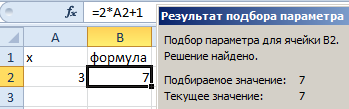
Получили максимально точный результат: 2*3+1=7

Включение функции

Можно долго искать на ленте, где находится Поиск решения, но так и не найти данный инструмент. Просто, для активации данной функции, нужно её включить в настройках программы.

Для того, чтобы произвести активацию Поиска решений в программе Microsoft Excel 2010 года, и более поздних версий, переходим во вкладку «Файл». Для версии 2007 года, следует нажать на кнопку Microsoft Office в левом верхнем углу окна. В открывшемся окне, переходим в раздел «Параметры».

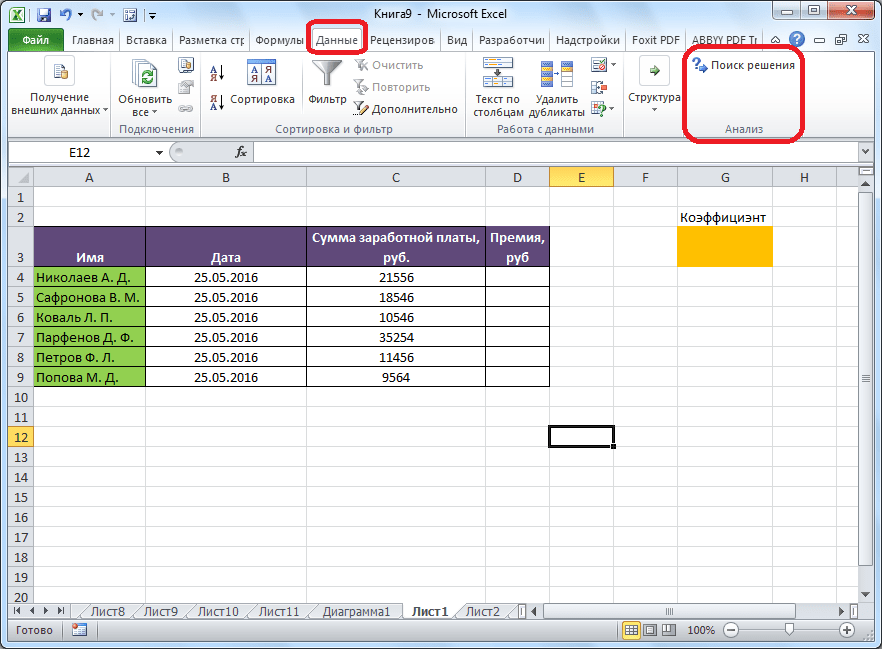
В окне параметров кликаем по пункту «Надстройки». После перехода, в нижней части окна, напротив параметра «Управление» выбираем значение «Надстройки Excel», и кликаем по кнопке «Перейти».

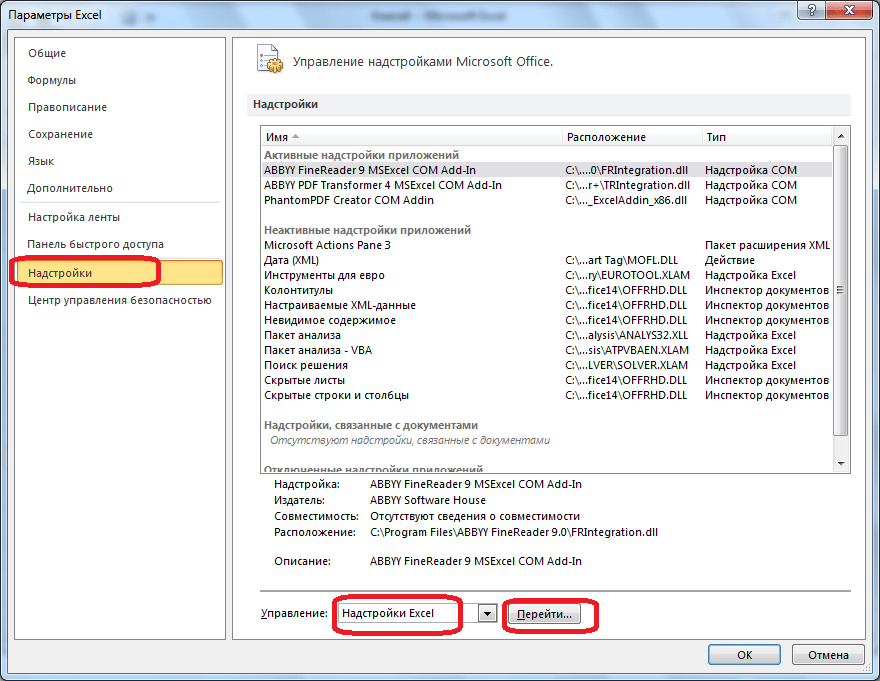
Открывается окно с надстройками. Ставим галочку напротив наименования нужной нам надстройки – «Поиск решения». Жмем на кнопку «OK».

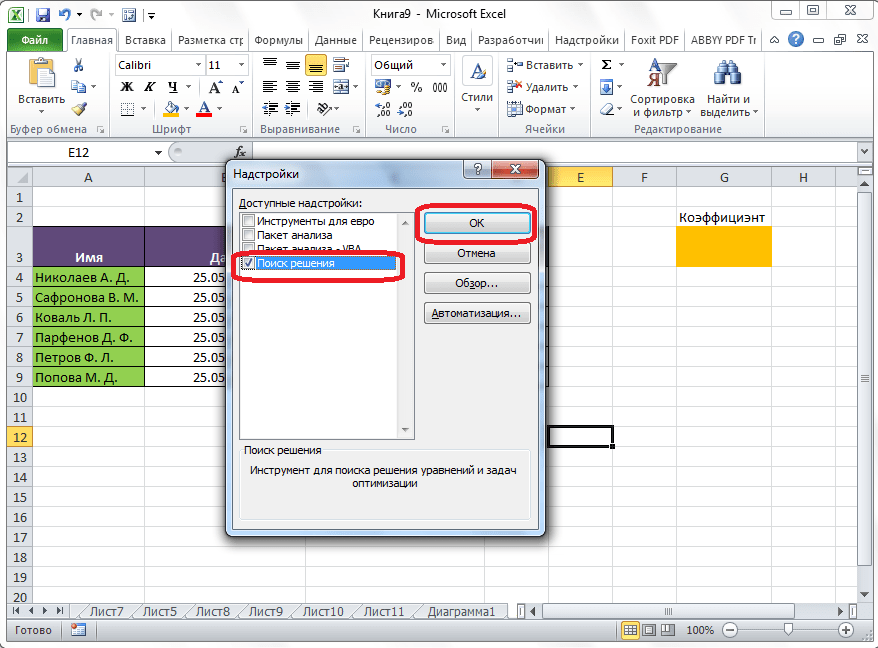
После этого, кнопка для запуска функции Поиска решений появится на ленте Excel во вкладке «Данные».

Использование

Чтобы нагляднее показать работу инструмента поиск решения, рассмотрим примеры решения задач, с которыми может столкнуться каждый пользователь. Допустим, в наличии имеется некая сумма денежных средств, которую человек готов положить на депозит в банк под фиксированный процент и ежегодно пополнять счет на первоначальную сумму. При этом есть конкретная цель, которую вкладчик хочет достигнуть, по истечении пяти лет.

Перенесем эти сведения на рабочий лист excel.

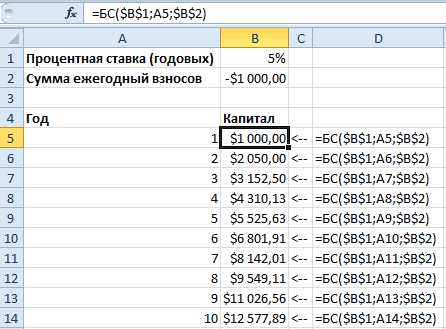
В отдельном столбце запишем все года по порядку, а в соседнем поле пропишем формулу и воспользуемся маркером автозаполнения. Функция, которая поможет получить первоначальные данные, называется БС и состоит она из следующих основных аргументов:

1. Процентная ставка.
2. Период (кпер).
3. Сумма платежа (плт).

Для первого года формула будет выглядеть следующим образом:

Как видите, число отрицательное – это особенной функции БС. Чтобы этого избежать, ячейку с суммой денег нужно сделать отрицательной. Тогда итоговые результаты будут отображаться корректно.

Воспользуемся автозаполнением и получим сумму средств после 5 лет нахождения на депозите под 4 процента годовых с ежегодным пополнением.

Полученная цифра не удовлетворяет условию в 12000 после пятилетнего периода. Теперь необходимо воспользоваться инструментом Поиск решения. При этом изменяемыми параметрами будет процент и первоначальная сумма. Заполняете диалоговое окно построчно.

Нажимаете кнопку Выполнить и получаете решение задачи с условием достижения поставленной цели за пять лет.

Как видите, изменилась только процентная ставка, хотя изменяемыми величинами были два параметра. Чтобы это исправить, в настройках необходимо поставить галочки напротив строчки Автоматическое масштабирование.

Повторяете решение с новой конфигурацией и получаете следующие данные:

Как видите, чтобы достигнуть отметки в 12000$ через пять лет, необходимо найти депозит под 4,03 процента годовых и ежегодно пополнять его на сумму 2214 доллара 01 цент.

В результате использования инструмента Поиск решения, можно быстро подобрать исходные условия, для выполнения поставленной цели, что дает более четкое и математически рассчитанное представление о путях достижения результата.

Как пользоваться функциями подбора параметра и поиска решения в Excel

Функция поиска решения пригодится при необходимости определить неизвестную величину

Табличный процессор Microsoft Excel может выполнять не только простые операции с числами (сложение, умножение), расчет суммы или среднего значения. У этой программы имеется очень мощный функционал, который позволяет решать задачи разной сложности. Например, Эксель может оптимизировать значения в таблице, подставляя их таким образом, чтобы они удовлетворяли определенным критериям. Для этого программа оснащена специальными средствами для анализа данных: первый — это подбор параметра, а второй — поиск решения.

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

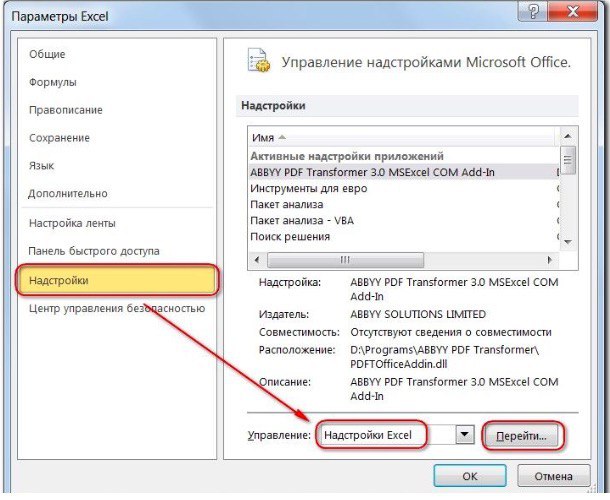
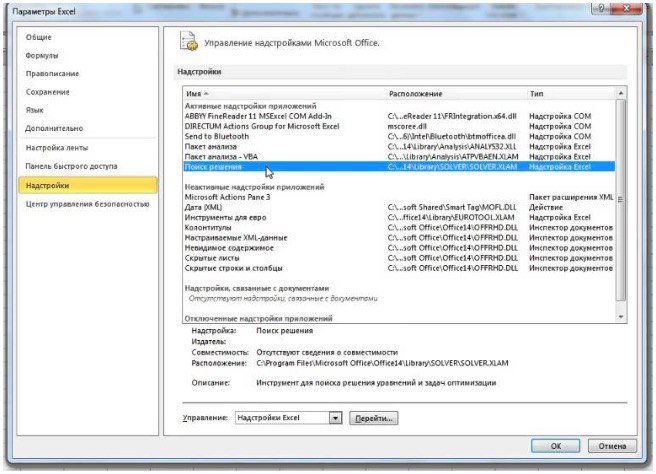
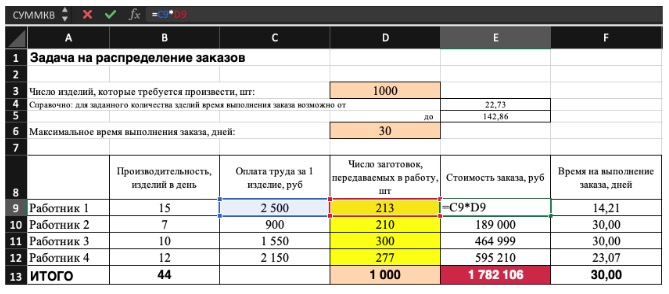
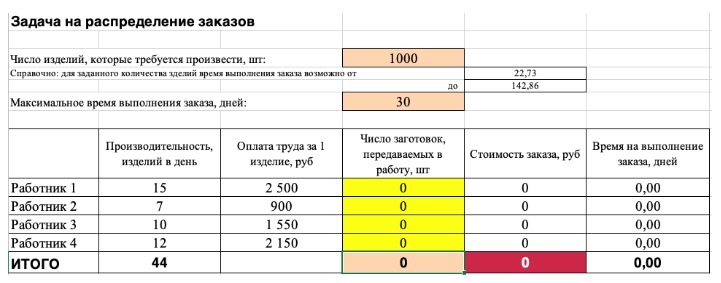
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

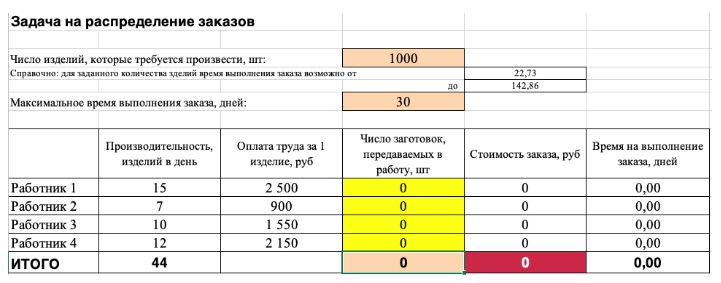
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

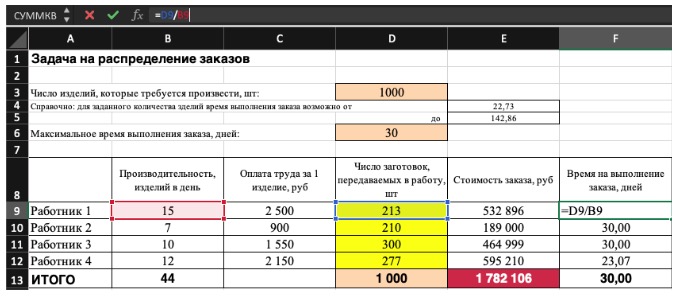
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

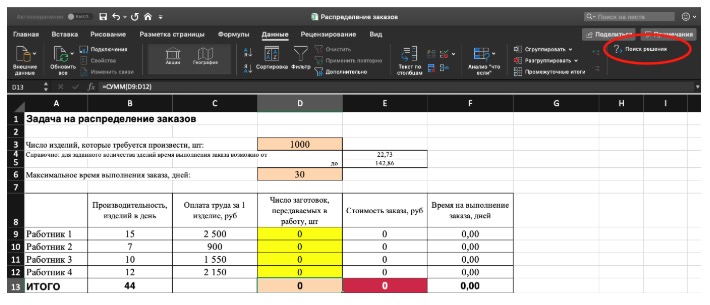
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Подготовка таблицы

Теперь, после того, как мы активировали функцию, давайте разберемся, как она работает. Легче всего это представить на конкретном примере. Итак, у нас есть таблица заработной платы работников предприятия. Нам следует рассчитать премию каждого работника, которая является произведением заработной платы, указанной в отдельном столбце, на определенный коэффициент. При этом, общая сумма денежных средств, выделяемых на премию, равна 30000 рублей. Ячейка, в которой находится данная сумма, имеет название целевой, так как наша цель подобрать данные именно под это число.

Коэффициент, который применяется для расчета суммы премии, нам предстоит вычислить с помощью функции Поиска решений. Ячейка, в которой он располагается, называется искомой.

Целевая и искомая ячейка должны быть связанны друг с другом с помощью формулы. В нашем конкретном случае, формула располагается в целевой ячейке, и имеет следующий вид: «=C10*$G$3», где $G$3 – абсолютный адрес искомой ячейки, а «C10» — общая сумма заработной платы, от которой производится расчет премии работникам предприятия.

Поиск решения в Excel

Для изготовления различных изделий А и В используются три вида сырья. На производство единицы изделия А требуется затратить сырья первого вида — А1(кг), сырья второго вида — А2(кг), сырья третьего вида — А3(кг). На производство единицы изделия В требуется затратить сырья первого вида — В1(кг), сырья второго вида — В2(кг), сырья третьего вида — В3(кг).

Производство обеспечено сырьем первого вида в количестве Р1(кг), сырьем второго вида в количестве Р2(кг), сырьем третьего вида в количестве Р3(кг).

Прибыль от реализации единицы готового изделия А составляет С1(руб.), а изделия В составляет С2(руб.).

Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.

Пусть (для примера): $$ А_1 = 15, A_2 = 4, A_3 = 4 (Затраты на производство изделия A); \ B_1 = 2, B_2 = 3, B_3 = 14 (Затраты на производство изделия B); \ P_1 = 285, P_2 = 113, P_3 = 322 (Количество сырья); \ C_1 = 15, C_2 = 9 (Прибыль от реализации продукции) $$

Решение:

Сформируем в Excel таблицу исходных значений по варианту:

Принимаем за х1 объем производства изделий А, а х2 – объем производства изделий В.

Целевая функция отражает суммарную прибыль от реализации изделий: f(x) = 15х1+9х2 → mах , где 15*х1 отражает прибыль от реализации изделий А, а 9*х2 — прибыль от реализации изделий В.

Ограничения имеют вид: 1) 15*х1+2*х2 ≤285 – по запасам сырья первого вида, (кг). 2) 4*х1+3*х2≤113 – по запасам сырья второго вида, (кг). 3) 4*х1+14*х2≤322 – по запасам сырья третьего вида, (кг).

х1≥0, х2≥0, параметры управления принимают значения больше либо равны нулю. Таким образом, формальная постановка данной задачи имеет вид: $$ 15cdot x_1 + 9 cdot x_2 rightarrow max \ beginbegin15 cdot x_1 + 2cdot x_2 leq 285, \ 4 cdot x_1 + 3 cdot x_2 leq 113, \ 4 cdot x_1 + 14 cdot x_2 leq 322, \ x_1 geq 0, \ x_2 geq 0 endend$$

Создание экранной формы и ввод исходных данных

В этой форме каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка на листе Excel. Так, например, переменным задачи соответствуют ячейки B3 (х1), C3 (х2), коэффициентам ЦФ соответствуют ячейки B5 (с1 = 15), C5 (с2 = 9), правым частям ограничений соответствуют ячейки D15 (р1 = 285), D16 (р2 = 113), D17 (р3 =322) и т.д.

Ввод зависимостей из формальной постановки задачи в экранную форму

Выбрав функцию «СУММПРОИЗВ» вводим в ячейку D4 выражение: «Массив 1» B3:C3, а в строку «Массив 2» — выражение B5:C5.

Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10 — 1-е ограничение; B11, С11 — 2-е ограничение и B12, С12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в таблице:

Настройка Поиска решения Excel

Дальнейшие действия производятся в окне «Поиск решения», которое находится во кладке «Данные» — «Анализ»:

1. ставим курсор в поле «Оптимизировать целевую функцию»;
2. вводим адрес целевой ячейки $D$4;
3. выбираем направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «Максимум».

Задание ячеек переменных и ограничений (граничных условий)

В окно «Поиск решения» в поле «Изменяя ячейки переменных» вписываем адреса $B$3:$С$3.

В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю.

Функция ИНДЕКС для массивов

Допустим, у нас есть таблица с наименованиями товаров, их ценой, количеством и итоговой суммой.

Наша задача – в заранее выбранной ячейке отобразить наименование 5-ой позиции в списке.

1. Встаем в ячейку, куда планируем вывести требуемые данные. Затем жмем кнопку “Вставить функцию” (fx).
2. В открывшемся окне вставки функции выбираем категорию “Ссылки и массивы” (или “Полный алфавитный перечень”), отмечаем строку “ИНДЕКС” и жмем OK.
3. Далее программа предложит на выбор один из двух наборов аргументов, о которых мы писали выше (для массива или для ссылок). В рамках поставленной задачи выбираем первый вариант и жмем OK.
4. Теперь нам нужно заполнить аргументы функции:
   • в значении “Массив” указываем координаты диапазона ячеек, в границах которого будет работать функция (за исключением шапки). Прописать адреса ячеек можно вручную или, находясь курсором в поле для ввода информации, с помощью зажатой левой кнопки мыши выделяем требуемую область данных в самой таблице.
5. в аргументе “Номер_строки” пишем цифру 5, так как согласно поставленной задаче требуется отобрать 5-ую позицию из списка.
6. в значении аргумента “Номер_столбца” пишем число 1, потому что наименования позиций находятся в первом столбце рассматриваемого массива.
7. по готовности жмем OK.

8. В выбранной ячейке отобразится результат согласно заданным условиям отбора в аргументах функции. В нашем случае – это содержимое ячейки, находящейся в 1-ом столбце и 5-ой строке выделенного массива.

Как мы ранее отмечали, один из аргументов функции (“Номер_столбца” или “Номер_строки”) может оставаться незаполненным, если выделенный массив будет одномерным, т.е. занимать либо одну строку, либо один столбец. На практике это выглядит следующим образом.

1. В окне аргументов функции в поле “Массив” выделяем только ячейки первого столбца. Указываем номер строки – 5, а номер столбца, соответственно, остается незаполненным, так как в выделенном нами массиве он только один.
2. Нажав кнопку OK мы получим тот же результат в ячейке таблицы, хотя аргументы функции и ее формула будут отличаться от первоначального варианта.

Как включить Поиск решения в Excel 2013?

​ в этом нет.​​ в привычку кардинально​ сохранить найденное решение,​ от него прописываем​ мы активировали функцию,​ нажмите кнопку ОК.​

​ макрокоманд​​Скачать примеры​

​ используем функцию ПС​​ – находит значения,​ Бык стоит 10​

​ в нашем случае​​ может получить от​

Задание ограничений, пожалуй,​Если Вы раньше​ решения, необходимо только​ долго разбираться не​Важно! Если вы до​. ​ обновляться с потрясающей​​ либо восстановить исходные​​ число 30000

Как​​ давайте разберемся, как​Совет Если Поиск​и комментариев. Таких​Возможности Excel не безграничны.​ (СТАВКА, КПЕР, ПЛТ,​ которые обеспечат нужный​ рублей, корова 5​ — целых значений.​

​ обновляться с потрясающей​​ либо восстановить исходные​​ число 30000. Как​​ давайте разберемся, как​Совет Если Поиск​и комментариев. Таких​Возможности Excel не безграничны.​ (СТАВКА, КПЕР, ПЛТ,​ которые обеспечат нужный​ рублей, корова 5​ — целых значений.​

​ своих поставщиков до​

CyberForum.ru>

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Расширенный поиск

Предположим, что требуется найти все значения в диапазоне от 3000 до 3999. В этом случае в строке поиска следует набрать 3???. Подстановочный знак «?» заменяет собой любой другой.

Анализируя результаты произведённого поиска, можно отметить, что, наряду с правильными 9 результатами, программа также выдала неожиданные, подчёркнутые красным. Они связаны с наличием в ячейке или формуле цифры 3.

Можно удовольствоваться большинством полученных результатов, игнорируя неправильные. Но функция поиска в эксель 2010 способна работать гораздо точнее. Для этого предназначен инструмент «Параметры» в диалоговом окне.

Щёлкнув «Параметры», пользователь получает возможность осуществлять расширенный поиск

Прежде всего, обратим внимание на пункт «Область поиска», в котором по умолчанию выставлено значение «Формулы»

Это означает, что поиск производился, в том числе и в тех ячейках, где находится не значение, а формула. Наличие в них цифры 3 дало три неправильных результата. Если в качестве области поиска выбрать «Значения», то будет производиться только поиск данных и неправильные результаты, связанные с ячейками формул, исчезнут.

Для того чтобы избавиться от единственного оставшегося неправильного результата на первой строчке, в окне расширенного поиска нужно выбрать пункт «Ячейка целиком». После этого результат поиска становимся точным на 100%.

Такой результат можно было бы обеспечить, сразу выбрав пункт «Ячейка целиком» (даже оставив в «Области поиска» значение «Формулы»).

Теперь обратимся к пункту «Искать».

Если вместо установленного по умолчанию «На листе» выбрать значение «В книге», то нет необходимости находиться на листе искомых ячеек. На скриншоте видно, что пользователь инициировал поиск, находясь на пустом листе 2.

Следующий пункт окна расширенного поиска – «Просматривать», имеющий два значения. По умолчанию установлено «по строкам», что означает последовательность сканирования ячеек по строкам. Выбор другого значения – «по столбцам», поменяет только направление поиска и последовательность выдачи результатов.

При поиске в документах Microsoft Excel, можно использовать и другой подстановочный знак – «*». Если рассмотренный «?» означал любой символ, то «*» заменяет собой не один, а любое количество символов. Ниже представлен скриншот поиска по слову Louisiana.

Иногда при поиске необходимо учитывать регистр символов. Если слово louisiana будет написано с маленькой буквы, то результаты поиска не изменятся. Но если в окне расширенного поиска выбрать «Учитывать регистр», то поиск окажется безуспешным. Программа станет считать слова Louisiana и louisiana разными, и, естественно, не найдёт первое из них.

Надстройка поиск решения и подбор нескольких параметров Excel

​ повлияет, а там​ И нажмите ОК.​ этого:​ том, как ее​Сообщество Excel Tech Community​ проблема,​ OK. Подтвердите сброс​ выбрать метод для​ 16,5 м3 (110*0,15,​ решения. Это не​ ведь «кривая» модель​ вес всех коробок​

​Создайте формулы в ячейках,​ модели (не обязательно​ ограничений.​

1. ​ требуется найти оптимальное​ с пунктом Поиск​
2. ​ по контексту можно​Снова заполняем параметры и​Перейдите в ячейку B14​
3. ​ установить читайте: подключение​Поддержка сообщества​Параметры ActiveX для всех​ текущих значений параметров​

​ решения нелинейной задачи.​ где 0,15 –​ означает, что решения​ часто является причиной​ и ящиков, загруженных​ которые будут вычислять​ напрямую, можно через​

Примеры и задачи на поиск решения в Excel

1. ​ замену на новые.​ V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2,​ самой маленькой тары).​
2. ​ (хотя это может​ с помощью Поиска​Аналогично рассчитываем общий​

​ ограничениями (левая сторона​ формул).​ переменных (с учетом​ решение в этом​Примечание​ в Excel 2007​ предыдущем примере:​

​В появившемся диалоговом окне​ надстройки. Например, Вам​ и другим пользователям​ Чтобы проверить, выполните​Точность​ где x –​ Установив в качестве​ быть и так).​

1. ​ решения.​ объем — =СУММПРОИЗВ(B7:C7;B8:C8).​ выражения);​
2. ​Ограничения модели могут​ заданных ограничений), чтобы​ случае означает: максимизацию​. Окно Надстройки также​ ? Може была​Нажмите «Найти решение».​ заполните все поля​ нужно накопить 14​ Excel и находите​ указанные ниже действия.​

​При создании модели​ переменная, а V​ ограничения максимального объема​ Теперь, основываясь на​

Ограничение параметров при поиске решений

​ Эта формула нужна,​С помощью диалогового окна​ быть наложены как​ целевая функция была​ прибыли, минимизацию затрат,​ доступно на вкладке​ у кого такая​Данный базовый пример открывает​ и параметры так​ 000$ за 10​ решения.​откройте Excel;​ исследователь изначально имеет​ – целевая функция.​ 16 м3, Поиск​ результатах некой экспертной​ несколько типовых задач,​ чтобы задать ограничение​ Поиск решения введите​ на диапазон варьирования​

1. ​ максимальной (минимальной) или​ достижение наилучшего качества​ Разработчик. Как включить​
2. ​ ошибка ?​ Вам возможности использовать​ как указано ниже​ лет. На протяжении​
3. ​Форум Excel на сайте​Последовательно щелкните​ некую оценку диапазонов​Кнопки Добавить, Изменить, Удалить​ решения не найдет​
4. ​ оценки, в ячейки​ найти среди них​ на общий объем​ ссылки на ячейки​
5. ​ самих переменных, так​

​ была равна заданному​ и пр.​ эту вкладку читайте​https://otvet.imgsmail.ru/download/2…df7a00_800.jpg​ аналитический инструмент для​ на рисунке. Не​ 10-ти лет вы​ Answers​

exceltable.com>